Выполнение лабораторных работ в курсе общей физики по разделу “Электричество и магнетизм” имеет цель не только углубить понимание основных законов электромагнетизма, но и познакомиться с их практическим применением.
В лаборатории электричества и магнетизма кафедры физики УГТУ-УПИ лабораторные работы разбиты на циклы в соответствии с используемыми методами измерений и законами, на которых они основаны. Это обстоятельство определило последовательность в описании лабораторных работ в настоящих указаниях.
В разделе I описаны лабораторные работы, основанные на законах постоянного тока, а также компенсационный и мостовой методы измерений электрических величин.
В разделе II изучаются электромагнитные колебания - незатухающие, затухающие, их сложение. Рассмотрены два метода определения частоты колебания в сети переменного тока.
В разделе III на примере баллистического метода и метода компенсации изучается явление электромагнитной индукции.
В разделе IV описана лабораторная работа по изучению движения заряженной частицы в электрическом и магнитном полях.
ИЗУЧЕНИЕ ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ МЕТАЛЛИЧЕСКИХ ПРОВОДНИКОВ
Лабораторная работа N12
В работе рассмотрены вопросы, связанные с протеканием электрического тока в металлических материалах, описан метод измерения электросопротивления проводников на основе использования моста Уитстона. Приведены расчетные формулы, схема электрической цепи и описан порядок оформления отчета.
1. Электрический ток в металлах
Электрический ток представляет собой упорядоченное, направленное движение электрических зарядов. В металлах носителями заряда являются свободные электроны, или электроны проводимости, отрицательно заряженные частицы, несущие элементарный заряд
Способность вещества проводить ток характеризуется удельной электрической проводимостью (электропроводностью) ![]() , которая обратнопропорциональна его удельному электрическому сопротивлению
, которая обратнопропорциональна его удельному электрическому сопротивлению ![]() . Значения r и s зависят от природы проводника и условий, при которых он находится, в частности, от температуры. Все металлы, находящиеся в твердой фазе, обладают кристаллической решеткой, которая никогда не бывает совершенной. Рассеяние электронов проводимости при их движении в металле, которое и приводит к возникновению электрического сопротивления R проводника, обусловлено тепловыми колебаниями решетки и ее дефектностью. Строгое объяснение механизма электропроводности металлов дает квантовая теория твердого тела.
. Значения r и s зависят от природы проводника и условий, при которых он находится, в частности, от температуры. Все металлы, находящиеся в твердой фазе, обладают кристаллической решеткой, которая никогда не бывает совершенной. Рассеяние электронов проводимости при их движении в металле, которое и приводит к возникновению электрического сопротивления R проводника, обусловлено тепловыми колебаниями решетки и ее дефектностью. Строгое объяснение механизма электропроводности металлов дает квантовая теория твердого тела.
В соответствии с законом Ома в интегральной форме сила тока ![]() , текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике
, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике
![]() (1)
(1)
причем, в данном случае ![]() совпадает с разностью потенциалов
совпадает с разностью потенциалов
![]() (2)
(2)
где ![]() - длина проводника,
- длина проводника,
![]()
Электрический ток характеризуется также с помощью вектора плотности тока, ![]() , который численно равен силе тока через расположенную в данной точке площадку, перпендикулярную к направлению движения носителей заряда, отнесенной к величине этой площадки,
, который численно равен силе тока через расположенную в данной точке площадку, перпендикулярную к направлению движения носителей заряда, отнесенной к величине этой площадки,
![]() . (3)
. (3)
Направление ![]() совпадает с направлением вектора напряженности электрического поля
совпадает с направлением вектора напряженности электрического поля ![]() в металлическом проводнике. Поскольку за направление тока условились принимать направление движения положительных зарядов, то вектор
в металлическом проводнике. Поскольку за направление тока условились принимать направление движения положительных зарядов, то вектор ![]() противоположен по направлению упорядоченному движению электронов в металле.
противоположен по направлению упорядоченному движению электронов в металле.
Согласно закону Ома в дифференциальной форме
![]() , (4)
, (4)
где
![]() . (5)
. (5)
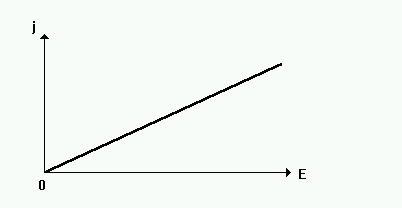
Таким образом, получив экспериментальную зависимость, приведенную на рис.1, можно определить ![]() образца по формуле
образца по формуле
![]() . (6)
. (6)
Классическая теория электропроводности предполагает, что электроны проводимости в металле ведут себя подобно молекулам идеального газа, сталкивающимся преимущественно не между собой, а с ионами, образующими кристаллическую решетку, что приводит к установлению теплового равновесия между электронным газом и кристаллической решеткой. Оценка средней скорости хаотического теплового движения электронов при комнатной температуре дает значение ![]() м/с.
м/с.
При включении электрического поля на хаотическое движение электронов накладывается упорядоченное движение со средней скоростью,
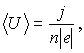 (7)
(7)
где ![]()
Для разных металлов значения ![]() м3. Приняв
м3. Приняв ![]() м3, легко оценить по формуле (7) величину
м3, легко оценить по формуле (7) величину ![]() и сравнить ее со значением
и сравнить ее со значением ![]() .
.
2. Расчет моста Уитстона на основе правил Кирхгофа
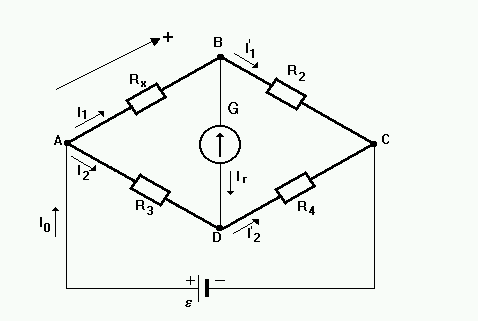
В настоящей работе определение сопротивления осуществляется как с использованием закона Ома в интегральной форме (1), так и при помощи моста постоянного тока, называемого мостом Уитстона.
Мост Уитстона (рис. 2) включает в себя четыре сопротивления, образующих своего рода четырехугольник, в одну диагональ которого включается источник тока ![]() , а в другую - гальванометр
, а в другую - гальванометр
Для облегчения расчетов разветвленных цепей разработан ряд вспомогательных приемов, один из которых основан на применении двух правил Кирхгофа.
Первое правило Кирхгофа относится к узлам цепи: алгебраическая сумма сходящихся в узле токов равна нулю
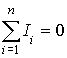 . (8)
. (8)
Правило знаков: втекающие в узел токи считаются положительными, вытекающие из него - отрицательными.
Второе правило Кирхгофа относится к отдельным замкнутым контурам разветвленной цепи: в любом замкнутом контуре алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС, встречающихся в этом контуре,
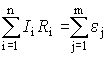 . (9)
. (9)
Для определения знаков в суммах выбирают положительное направление обхода контура. Правило знаков: ток, совпадающий по направлению с направлением обхода, считается положительным; ЭДС ![]() , потенциал которой возрастает в направлении обхода, также входит в уравнение (9) со знаком "+". Уравнение (9) можно составить для любых независимых замкнутых контуров в данной разветвленной цепи.
, потенциал которой возрастает в направлении обхода, также входит в уравнение (9) со знаком "+". Уравнение (9) можно составить для любых независимых замкнутых контуров в данной разветвленной цепи.
Рассчитаем схему моста Уитстона на основе правил Кирхгофа. Выбираем направление токов так, как показано на рис. 2. Обходить контуры будем по часовой стрелке. Для определения искомого сопротивления
R x достаточно написать следующие уравнения Кирхгофа:![]() = 0 - для узла В;
= 0 - для узла В;
![]() = 0 - для узла D;
= 0 - для узла D;
![]() = 0 - для контура ABDA;
= 0 - для контура ABDA;
![]() = 0 - для контура BCDB,
= 0 - для контура BCDB,
где R - сопротивление гальванометра.
Для измерения сопротивления ![]() с помощью моста Уитстона сопротивления
с помощью моста Уитстона сопротивления ![]() и
и ![]() подбираются таким образом, чтобы ток через гальванометр был равен нулю (I
подбираются таким образом, чтобы ток через гальванометр был равен нулю (I
Решая эту систему уравнений, получаем формулу для определения ![]()
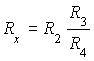 . (11)
. (11)
3. Применение реохорда в схеме моста Уитстона
В соответствии с рис. 2 и формулой (11) для определения ![]() необходимо знать
необходимо знать ![]() и отношение
и отношение ![]() . Это отношение может быть заменено отношением величин, пропорциональных сопротивлениям, что и осуществляется в данной работе.
. Это отношение может быть заменено отношением величин, пропорциональных сопротивлениям, что и осуществляется в данной работе.
В рабочей схеме (рис. 3) ветвью ADC является калиброванная проволока реохорда. Вдоль реохорда перемещается скользящий по проволоке контакт
D, благодаря которому можно изменять соотношение сопротивлений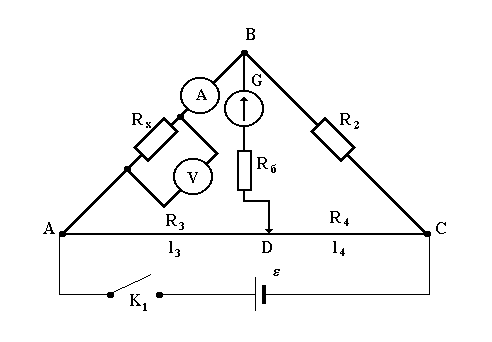
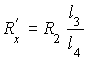 . (12)
. (12)
Рис. 3. Рабочая схема установки
Здесь ![]() представляет собой сумму последовательно соединенных сопротивления
представляет собой сумму последовательно соединенных сопротивления ![]() и сопротивления амперметра
и сопротивления амперметра ![]() , которое всегда должно быть много меньше, чем значение
, которое всегда должно быть много меньше, чем значение ![]()
Таким образом, измерение сопротивления ![]() мостовым методом связано с определением длин плеч реохорда
мостовым методом связано с определением длин плеч реохорда ![]() и
и ![]() сбалансированного моста при известном сопротивлении
сбалансированного моста при известном сопротивлении ![]()
В данной работе используется реохорд барабанного типа, в котором однородная проволока намотана по цилиндрической спирали. В этом случае длина проволоки на участке AD равна ![]() , где
, где ![]() - длина одного витка проволоки,
- длина одного витка проволоки, ![]() - число витков на участке AD. Длина проволоки на участке DC равна
- число витков на участке AD. Длина проволоки на участке DC равна ![]() , где
, где ![]() - число витков на участке DC. Подставляя
- число витков на участке DC. Подставляя ![]() и
и ![]() в выражение (12), получим расчетную формулу для определения
в выражение (12), получим расчетную формулу для определения ![]()
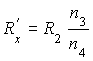 . (13)
. (13)
Величину сопротивления ![]() лучше подбирать такой, чтобы при окончательной балансировке моста скользящий контакт
лучше подбирать такой, чтобы при окончательной балансировке моста скользящий контакт
Параллельно сопротивлению ![]() подсоединен вольтметр, внутреннее сопротивление которого на несколько порядков выше значения
подсоединен вольтметр, внутреннее сопротивление которого на несколько порядков выше значения ![]() . Поэтому ток, текущий через вольтметр при сбалансированном мосте, практически равен нулю. Вольтметр же показывает падение напряжения
. Поэтому ток, текущий через вольтметр при сбалансированном мосте, практически равен нулю. Вольтметр же показывает падение напряжения
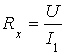 . (14)
. (14)
Зная ![]() и
и ![]() , можно легко определить и сопротивление амперметра
, можно легко определить и сопротивление амперметра ![]()
![]() . (15)
. (15)
Строго говоря, ![]() включает в себя и сопротивление соединительных проводов на участке AB (рис. 3).
включает в себя и сопротивление соединительных проводов на участке AB (рис. 3).
B заключение отметим, что с помощью описанного метода нельзя определять с достаточной точностью слишком малые сопротивления. Это связано с тем, что начинает сказываться сопротивление контактов и подводящих проводов, а также нагревание плеч моста при прохождении по ним тока.
Схема электрической цепи моста представлена на рис.3. ![]() -сопротивление калиброванной проволоки, которое следует определить (длина и диаметр проволоки указаны на панели, к которой крепится проволока). A - амперметр (или миллиамперметр), показывающий текущий по
-сопротивление калиброванной проволоки, которое следует определить (длина и диаметр проволоки указаны на панели, к которой крепится проволока). A - амперметр (или миллиамперметр), показывающий текущий по ![]() ток; сопротивление амперметра
ток; сопротивление амперметра ![]() вычисляется по формуле (15). V - вольтметр, регистрирующий падение напряжения на
вычисляется по формуле (15). V - вольтметр, регистрирующий падение напряжения на ![]() . В качестве плеча
. В качестве плеча ![]() используется магазин сопротивления.
используется магазин сопротивления.
Ветвью ADC является реохорд барабанного типа, в котором однородная калиброванная проволока намотана по цилиндрической спирали на барабан. Подвижным контактом является ролик, осью которого служит прямолинейный стержень. При вращении барабана ролик, будучи сцепленным с витками проволоки, перемещается вдоль стержня. Положение ролика относительно барабана определяется с помощью двух шкал - линейной и круговой. Линейная шкала расположена непосредственно под роликом, цена ее деления соответствует длине одного витка проволоки (или одному обороту), т.к. при одном обороте барабана ролик смещается вдоль шкалы на одно деление. Круговая шкала, разделенная на 100 частей, нанесена на торце барабана; цена деления этой шкалы соответствует 0,01 части длины витка проволоки (или 0,01 оборота).
Нуль-гальванометр
G включается в диагональ моста последовательно с балластным сопротивлением R б, служащим для защиты гальванометра от перегрузки. Источником тока служит батарея ![]() , включенная в цепь последовательно с ключом К. Во избежание перегрева плеч моста ток в цепи должен быть минимальным.
, включенная в цепь последовательно с ключом К. Во избежание перегрева плеч моста ток в цепи должен быть минимальным.
1. Составить перечень приборов и указать их характеристики, заполнив табл. П.1.
2. Ввести полностью сопротивление
R б, при этом ключ К должен быть разомкнут.3. Установить на магазине значение сопротивления R2 = 20 Ом.
4. Выполнить измерения ![]() . Для этого замкнуть ключ К и сбалансировать мост путем перемещения контакта D вдоль реохорда при постепенном выведении балластного сопротивления R б из цепи гальванометра. Когда стрелка гальванометра установится на нуле, записать показания вольтметра и амперметра, разомкнуть ключ К и отсчитать значения
. Для этого замкнуть ключ К и сбалансировать мост путем перемещения контакта D вдоль реохорда при постепенном выведении балластного сопротивления R б из цепи гальванометра. Когда стрелка гальванометра установится на нуле, записать показания вольтметра и амперметра, разомкнуть ключ К и отсчитать значения ![]() и
и ![]() .
.
Измерения ![]() повторить еще четыре раза, увеличивая каждый раз значения
повторить еще четыре раза, увеличивая каждый раз значения ![]() на 10 Ом. Результаты всех измерений занести в табл.П.2.
на 10 Ом. Результаты всех измерений занести в табл.П.2.
5. По формуле (13) произвести расчеты ![]() и результаты занести в табл.П.2.
и результаты занести в табл.П.2.
6. По выражению (14) рассчитать ![]() , занести в табл.П.2 и найти среднее значение
, занести в табл.П.2 и найти среднее значение ![]() . Полученный результат сравнить с контрольными данными.
. Полученный результат сравнить с контрольными данными.
7. По формуле (15) найти ![]() , записать в табл.П.2 и определить среднее значение
, записать в табл.П.2 и определить среднее значение ![]() . Полученный результат сравнить с контрольными данными.
. Полученный результат сравнить с контрольными данными.
8. По формуле
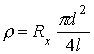 , (16)
, (16)
где
d - диаметр проволоки, определить значение удельного сопротивления проволоки и сравнить его с контрольными данными.9. По формуле
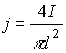 (17)
(17)
произвести расчеты плотности тока и результаты занести в табл.2.
10. По выражению (5) рассчитать значения напряженности электрического поля
E в проводнике
11. На миллиметровой бумаге построить график
j = f(E), по формуле (6) определить значение r гр, сравнить его с контрольными данными и со значением12. По формуле (7) оценить значения <U> для разных величин плотностей тока и результаты занести в табл. П.2.
13. Произвести расчеты погрешностей в определении ![]() и
и ![]() .
.
14. Оформить отчет согласно "Приложению".
Контрольные вопросы
1. Что представляет собой электрический ток? Какие частицы являются cвободными носителями заряда в металлах?
2. Какова причина электрического сопротивления при протекании тока в металлах?
3. Сформулировать закон Ома для однородного участка цепи в интегральной и дифференциальной формах.
4. Существует ли движение носителей заряда в металлическом проводнике при отсутствии в нем электрического поля? Если да, то какое?
5. Какое направление принимается за направление тока?
6. Почему амперметр включается в электрическую цепь последовательно, а вольтметр - параллельно?
7. Какие цепи называются мостами постоянного тока?
8. Сформулировать первое правило Кирхгофа.
9. Сформулировать второе правило Кирхгофа. Для чего необходимо выбирать направление обхода контура?
10. Какова принципиальная схема работы моста постоянного тока? В чем заключается принцип ее работы?
ФОРМА ОТЧЕТА
Титульный лист
У Г Т У - У П И
Кафедра физики
ОТЧЕТ
по лабораторной работе N 12
“Изучение электрического сопротивления металлических
проводников”
Студент(ка)-___
_________________Группа ________________________
Дата __________________________
На внутренних страницах:
1.Расчетные формулы:
1.1. Формула для расчета величины ![]()
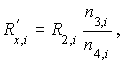
где ![]() - известное сопротивление;
- известное сопротивление;
![]() - числа витков (оборотов) реохорда, соответствующие плечам
- числа витков (оборотов) реохорда, соответствующие плечам ![]() и
и ![]() .
.
1.2. Формулы для расчета величины ![]()
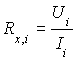 ,
,
где ![]() - показания вольтметра,
- показания вольтметра, ![]() - показания амперметра.
- показания амперметра.
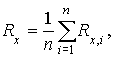
где
n - число измерений.1.3. Формулы для определения значения ![]()
![]()
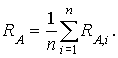
1.4. Формула для определения удельного электросопротивления
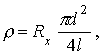
где
d - диаметр исследуемого проволочного образца; l - длина проволоки.1.5. Формула для расчета плотности тока
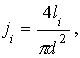
где
Ii - текущий по образцу ток.1.6. Формула для расчета напряженности электрического поля
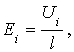
где
Ui - падение напряжения на образце.1.7. Формула для определения значения удельного электросопротивления по данным графика
j = f(E)r
гр1.8. Формула для оценки средней скорости направленного движения электронов в образце
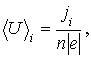
где ![]() м
м
![]() Кл - величина заряда электрона.
Кл - величина заряда электрона.
2.Схема рабочей цепи
3. Средства измерений и их характеристики
Таблица П.1
|
Наименование средства измерения |
Предел измерения |
Цена деления шкалы |
Класс точ-ности |
Предел основной погрешности, |
|
Реохорд высокоомный барабанного типа: линейная шкала круговая шкала Нуль-гальванометр Вольтметр Амперметр Магазины сопротивлений: R 2R б Реостат движковый |
Исследуемое сопротивление №_____
l
= .........., м , D l =............,м,d
= ..........,м, D d = ..........,м.4. Результаты измерений и расчетные значения
Таблица П. 2
|
N п/п |
R2 , Ом |
n3, Об |
n4, Об |
R’x, Ом |
l, А |
U ,B |
Rx, Ом |
RA ,Ом |
E, B/ м |
j, A/м 2 |
<U>, м/c |
|
1 |
20 |
|
|
|
|
|
|
|
|
|
|
|
2 |
30 |
|
|
|
|
|
|
|
|
|
|
|
3 |
40 |
|
|
|
|
|
|
|
|
|
|
|
4 |
50 |
|
|
|
|
|
|
|
|
|
|
|
5 |
60 |
|
|
|
|
|
|
|
|
|
|
5. Расчеты искомых величин:
5.1 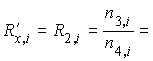
5.2.![]()
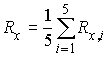 = ...................Ом.
= ...................Ом.
5.3.![]()
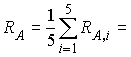 ..................Ом.
..................Ом.
5.4. ![]()
5.5. 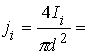
5.6.![]() ....................В/м.
....................В/м.
5.7.
r гр = 5.8. 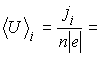
6.Оценка границ погрешностей
6.1. Результаты измерения ![]()
Таблица П.3
|
N п/п |
|
|
|
|
1 2 3 4 5 |
|
|
|
Cреднее значение ![]() =.....................Ом.
=.....................Ом.
 = .....................Ом;
= .....................Ом;
![]() коэффицент Стьюдента, значение которого берется из таблицы.
коэффицент Стьюдента, значение которого берется из таблицы.
![]() .................Ом;
.................Ом;
![]() ..................Ом при Р=0,95.
..................Ом при Р=0,95.
6.2. Результаты измерения ![]()
Таблица П.4
|
N п/п |
|
|
|
|
1 2 3 4 5 |
|
|
|
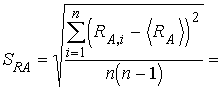 .......................Ом;
.......................Ом;
![]() .....................Ом;
.....................Ом;
![]() ...................Ом при Р = 0,95.
...................Ом при Р = 0,95.
6.3. Результаты расчета
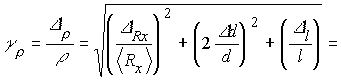 ........................;
........................;
![]() ...............ОмЧ м при Р=0,95.
...............ОмЧ м при Р=0,95.
7.Окончательные результаты
R
x =...................Ом при P = 0,95;R A =..................Ом при P = 0,95;
r
= ....................ОмЧ м при P = 0,95;r
гр = .................ОмЧ м;б
Uс 1 = м/c;б
Uс 5 = м/c.8.
Выводы.